Since “Carlos Hidalgo & Asociados” group suggests (they haven't ruled out the possiblility) the inner structure of Veas-01 could well be the Hexagonal Close-Packed (HCP) for iron formed at very high pressures, and for educational purposes, here is described (for 17 elemental metals) some similarities and differences between Face Centered Cubic (FCC) and HCP structure.
Clearly, the 17 elements below described was forming at room pressure, which is quite different from what happens for HCP for Fe. To form the closest structure ever seen for iron atoms, and according to first-principles modelling of Earth and planetary materials, you should supposedly have iron at pressures in the megabar region (1 Mbar = 100 GPa) and temperatures of several thousand Kelvin. Since owners of Veas-01 are currently waiting for analysis concerning its crystalline structure (using the Transmission Electron Microscope, TEM, adquired by Universidad de Chile), and for general purposes, it is reviewed some possible volumes and its interatomic distances between Fe atoms considering pressures up to 200 GPa.
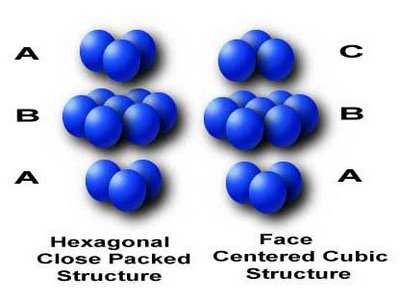
Similarities and Differences Between the FCC and HCP Structure
The face centered cubic and hexagonal close packed structures both have a packing factor of 0.74, consist of closely packed planes of atoms, and have a coordination number of 12. The difference between the fcc and hcp is the stacking sequence. The hcp layers cycle among the two equivalent shifted positions whereas the fcc layers cycle between three positions. As can be seen in the image, the hcp structure contains only two types of planes with an alternating ABAB arrangement. Notice how the atoms of the third plane are in exactly the same position as the atoms in the first plane. However, the fcc structure contains three types of planes with a ABCABC arrangement. Notice how the atoms in rows A and C are no longer aligned. Remember that cubic lattice structures allow slippage to occur more easily than non-cubic lattices, so hcp metals are not as ductile as the fcc metals.
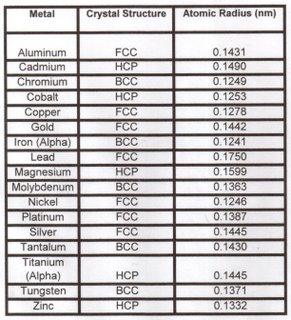
The table below shows the stable room temperature crystal structures for several elemental metals.
A nanometer (nm) equals 10E(-9) meter or 10 Angstrom units.
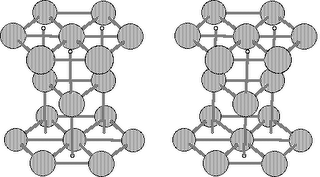
Hexagonal Close-Packed for Iron
Our present understanding of planetary interiors has been patched together from many disciplines, including astronomy, meteoritics, nuclear physics, material science and crystallography. Laboratory experiments at high pressures and temperatures provide invaluable information about the physical and chemical properties of the materials that are believed to make up the planets. Today, atomic-scale materials modelling based on first principles quantum mechanics is playing an important role in the science of the Earth and the other planets.
Nevertheless, there are considerable discrepancies between first-principles modelling and laboratory experiments.
Currently, there are three (3) main methods or techniques for performing experiments at pressures and temperatures relevant to planetary interiors, and for achieving these thermodynamic conditions:
a).- Multi-anvil high pressure cells, developed in Japan during the 70’s, enable pressures of 25 – 30 GPa and temperatures of up to 2000 K to be reached. This technique is ideal for crystal synthesis and for the study of phase equilibria.
b).- DAC, that means Diamond Anvil Cells. This method is better for obtaining higher pressures and temperatures. The transparency of diamond means that DACs can be coupled with laser heating of the sample to attain pressures of about 200 GPa and temperatures up to 6000 K. This enables the conditions within the Earth’s outer core to be reproduced. Diamond is also translucent to X-rays, so that laser heated DACs can be used with synchrotron X-ray radiation to determine the equations of state of planetary materials.
c).- Shock Experiments. This is the third approach to generating high pressures, in which a high-velocity projectile is fired into a target, and the Rankine-Hugoniot relations are used to determine the shock pressure. Shock experiments sample the Hugoniot trajectory through pressure-temperature space, and the temperature of the sample can be estimated from the Mie-Grüneisen equation. This, however, requieres a knowledge of the high p-T heat capacity and the Grüneisen parameter of the sample, both of which may be poorly known.
Although major advances have been made with all of this techniques, the problem of determining p and T at extreme conditions has led in some cases to discrepancies between different experimental approaches.
To give an example, the estimated melting of iron at 300 GPa as inferred by b) and c) studies differs by some 2000 K.
Difficulties such as this provide a strong incentive for finding or discovering new kind of unclassified siderites (iron meteorites), coming from the inner core of a planets similar to the Earth’ core diameter, in order to show evidence and provide new insights into the methods above described.
VOLUME AND Fe-ATOMIC DISTANCES IN HCP
The following figure shows the ideal hexagonal close-packed for iron:
Nevertheless, the main question that the reader could be made is: what would be the atomic distances and the corresponding volume for HCP-Fe?
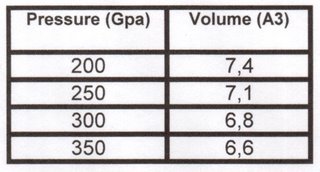
A couple of days ago, the physicist and geologist Dr. Gerd Steinle-Neumann, “Akademischer Rat” at the Bayerisches Geoinstitut in Germany, sent to us some possible volumes and distances for hcp-Fe taking into consideration pressures up to 200 GPa.
Using the method and predictions achieved by Dr. Steinle-Neumann, the following pressures (first column, in GPa) correspond to the following atomic volumes (second column, in cubic Angstroms)
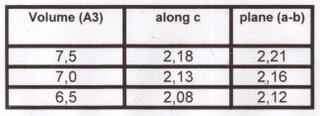
He gave us the atomic distances (in Angstroms) for some volumes. The different values are for out of plane (along c) and in plane (a-b), due to the non ideal packing of the close packed layers (c/a=1.6 in the computations, and from experiment at high P compared to the geometric value, of 1.633).
For further information about Dr. Steile-Neumann’s publications, please visit the following web site: