Hexagonal Close-Packed for Iron

Introduction

Since “Carlos Hidalgo & Asociados” group suggests (they haven't ruled out the possiblility) the inner structure of Veas-01 could well be the Hexagonal Close-Packed (HCP) for iron formed at very high pressures, and for educational purposes, here is described (for 17 elemental metals) some similarities and differences between Face Centered Cubic (FCC) and HCP structure.

Clearly, the 17 elements below described was forming at room pressure, which is quite different from what happens for HCP for Fe. To form the closest structure ever seen for iron atoms, and according to first-principles modelling of Earth and planetary materials, you should supposedly have iron at pressures in the megabar region (1 Mbar = 100 GPa) and temperatures of several thousand Kelvin. Since owners of Veas-01 are currently waiting for analysis concerning its crystalline structure (using the Transmission Electron Microscope, TEM, adquired by Universidad de Chile), and for general purposes, it is reviewed some possible volumes and its interatomic distances between Fe atoms considering pressures up to 200 GPa.

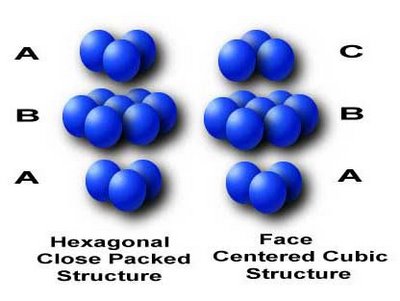
Similarities and Differences Between the FCC and HCP Structure

The face centered cubic and hexagonal close packed structures both have a packing factor of 0.74, consist of closely packed planes of atoms, and have a coordination number of 12. The difference between the fcc and hcp is the stacking sequence. The hcp layers cycle among the two equivalent shifted positions whereas the fcc layers cycle between three positions. As can be seen in the image, the hcp structure contains only two types of planes with an alternating ABAB arrangement. Notice how the atoms of the third plane are in exactly the same position as the atoms in the first plane. However, the fcc structure contains three types of planes with a ABCABC arrangement. Notice how the atoms in rows A and C are no longer aligned. Remember that cubic lattice structures allow slippage to occur more easily than non-cubic lattices, so hcp metals are not as ductile as the fcc metals.

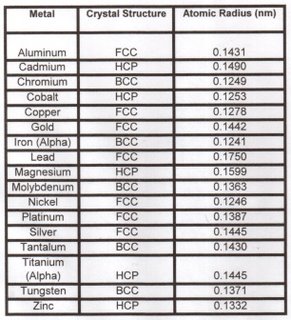
The table below shows the stable room temperature crystal structures for several elemental metals.

A nanometer (nm) equals 10E(-9) meter or 10 Angstrom units.

Hexagonal Close-Packed for Iron

Our present understanding of planetary interiors has been patched together from many disciplines, including astronomy, meteoritics, nuclear physics, material science and crystallography. Laboratory experiments at high pressures and temperatures provide invaluable information about the physical and chemical properties of the materials that are believed to make up the planets. Today, atomic-scale materials modelling based on first principles quantum mechanics is playing an important role in the science of the Earth and the other planets.

Nevertheless, there are considerable discrepancies between first-principles modelling and laboratory experiments.

Currently, there are three (3) main methods or techniques for performing experiments at pressures and temperatures relevant to planetary interiors, and for achieving these thermodynamic conditions:

a).- Multi-anvil high pressure cells, developed in Japan during the 70’s, enable pressures of 25 – 30 GPa and temperatures of up to 2000 K to be reached. This technique is ideal for crystal synthesis and for the study of phase equilibria.

b).- DAC, that means Diamond Anvil Cells. This method is better for obtaining higher pressures and temperatures. The transparency of diamond means that DACs can be coupled with laser heating of the sample to attain pressures of about 200 GPa and temperatures up to 6000 K. This enables the conditions within the Earth’s outer core to be reproduced. Diamond is also translucent to X-rays, so that laser heated DACs can be used with synchrotron X-ray radiation to determine the equations of state of planetary materials.

c).- Shock Experiments. This is the third approach to generating high pressures, in which a high-velocity projectile is fired into a target, and the Rankine-Hugoniot relations are used to determine the shock pressure. Shock experiments sample the Hugoniot trajectory through pressure-temperature space, and the temperature of the sample can be estimated from the Mie-Grüneisen equation. This, however, requieres a knowledge of the high p-T heat capacity and the Grüneisen parameter of the sample, both of which may be poorly known.

Although major advances have been made with all of this techniques, the problem of determining p and T at extreme conditions has led in some cases to discrepancies between different experimental approaches.

To give an example, the estimated melting of iron at 300 GPa as inferred by b) and c) studies differs by some 2000 K.

Difficulties such as this provide a strong incentive for finding or discovering new kind of unclassified siderites (iron meteorites), coming from the inner core of a planets similar to the Earth’ core diameter, in order to show evidence and provide new insights into the methods above described.

VOLUME AND Fe-ATOMIC DISTANCES IN HCP

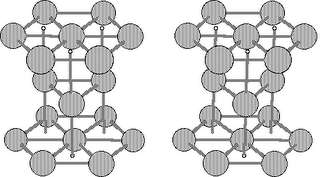
The following figure shows the ideal hexagonal close-packed for iron:

Nevertheless, the main question that the reader could be made is: what would be the atomic distances and the corresponding volume for HCP-Fe?

A couple of days ago, the physicist and geologist Dr. Gerd Steinle-Neumann, “Akademischer Rat” at the Bayerisches Geoinstitut in Germany, sent to us some possible volumes and distances for hcp-Fe taking into consideration pressures up to 200 GPa.

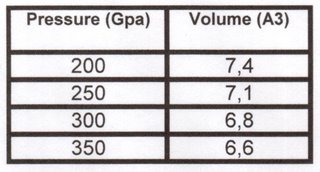
Using the method and predictions achieved by Dr. Steinle-Neumann, the following pressures (first column, in GPa) correspond to the following atomic volumes (second column, in cubic Angstroms)

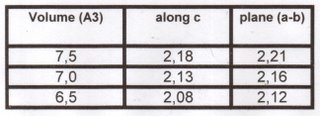
He gave us the atomic distances (in Angstroms) for some volumes. The different values are for out of plane (along c) and in plane (a-b), due to the non ideal packing of the close packed layers (c/a=1.6 in the computations, and from experiment at high P compared to the geometric value, of 1.633).

For further information about Dr. Steile-Neumann’s publications, please visit the following web site:

http://www.bgi.uni-bayreuth.de/

MAXIMO PRODUCTO BxH POR DOLAR

Cuando se desea comparar distintos materiales magéticos entre sí, y a la vez, conocer la aceptación o penetración de ellos en el mercado, a menudo la mejor figura que describe el “mérito” de dicho material lo da la expresión del "Máximo Producto BxH por Dolar":

(BH)max/USD

El Dr. José Luis Giordano, investigador de la Universidad de Talca, explica claramente, en sus publicaciones, el concepto implicado en esta relación. Un material, por ejemplo, requerido para fabricar imanes permanentes debe ser resistente a la desmagnetización. De esta manera, los materiales que poseen una fuerte resistencia a desmagentizarse se les denomina “Materiales Magnéticos Duros”. Para éstos las dos características escenciales corresponden a la Temperatura de Curie, Tc y al máximo producto BxH.

Un material que posea una alta Temperatura de Curie, Tc, funcionará perfectamente para sus objetivos también a altas temperaturas (siempre que T sea menor a Tc), sin destruirse sus propiedades magnéticas. Por otro lado, un mayor valor de (BH)max permite que el imán pueda tener un menor tamaño para una determinada aplicación.

No obstante, si lo que se desea es fabricar un perfecto núcleo de transformador o un electroimán, entonces se requerirán materiales que facilmente puedan desmagnetizarse, es decir, los llamados “Materiales Magnéticos Blandos”. Esto implica un (BH)max inferior a los valores obtenidos para los materiales “duros”.

Sin embargo, y en relación a las aplicaciones en el mercado, se obtiene una mejor cotización del material magnético cuanto más alto sea el valor de BxH dentro de la relación antes inicada, (BH)max/ USD. Es por ello que, para numerosas aplicaciones se llegan a preferir materiales duros como es el caso de algunas ferritas, pues éstas suelen ser menos costosas que algunos alnicos (éstos últimos son “mas duros” que ciertas ferritas).

Por lo anteriormente expresado, los parámetros que un fabricante entrega, referente a los materiales magnéticos que fabrica, además de la Temperatura de Curie Tc y el (BH)max, están los valores para la “Magnetización Remanente” (Mr) y para la “Coercitividad Intrínseca” (Hci). Evidentemente, el “Campo Remanente” o simplemente “Remanencia” se calculará como el producto entre la Permeabilidad Magnética del Vacío y la Magnetización Remanente.

Más, ¿cómo se determinan y entienden los valores Mr, Hci y (BH)max?. La respuesta se encuentra en el Ciclo de Histéresis Magnética.

CICLO DE HISTERESIS MAGNETICA

A continuación, y usando la curva mostrada abajo, describiremos la respuesta magnética de un Metal Ferromagnético o el de una Cerámica Ferrimagnética cuando le es aplicado un campo magnético externo H, respondiendo el material con lo que se denomina Magnetización M. Así, el ciclo M(H) representa la Magnetización M en función de campo aplicado H.

En un comienzo, cuando el material no ha sufrido estrés magnético (material "virgen"), tendremos un M = 0 (punto [1]). Cuando se aplica un campo magnético H, el material responde con la llamada “Curva de Primera Magnetización”, que une los puntos [1] y [2]. Al alcanzarse el punto [2] la magnetización alcanza su máximo valor, denominado “Magnetización de Saturación” Ms, y corresponde al fenómeno en donde los momentos magnéticos alcanzan su máxima alineación posible. Este parámetro es importante toda vez que muestra cuánta magnetización inducida puede tener un “imán temporal” cuando es excitado.

Si luego disminuimos la intensidad de H hasta alcanzar el valor cero, la magnetización M vuelve por valores mayores que los alcanzados en el proceso primero. Este fenómeno se observa entre los puntos [2] y [3], y su explicación se halla en el reordenamiento de los dominios, donde el material pareciese tener “memoria” de haber sido sometido a campos magnéticos superiores. Esta irreversibilidad de la magnetización se conoce como “Histéresis Magnética” del material. Al llegar al punto [3], en ausencia de campo efectivo, el material queda con una “Remanencia” Mr, conocida como “Magnetización Remanente”. Si este valor es multiplicado por el valor de la Permeabilidad Magnética en el vacío, se obtiene la consabida “Remanencia” Br. La importancia de este parámetro radica en el hecho que muestra cuánta magnetización puede almacenar un imán permanente.

Al aumentar el campo H en el sentido opuesto, entre la “Remanencia” y donde M = 0, se obtiene la curva entre los puntos [3] y [4], denominada “Curva de Desmagnetización” del material. La intensidad del campo H necesaria para anular M, se denomina “Coercitividad Intrínseca” o simplemente “Coercitividad” Hci. Para un imán, este es el parámetro más importante, porque representa su resistencia a ser desmagnetizado, además de que permite estimar cuál es la intensidad de campo necesaria para magnetizar el material, que desde un punto de vista práctico, equivale a una 5 veces el valor de la Coercitividad, Hci.

En esta Curva de Desmagnetización, existe un valor de H para el cual el material magnético posee el máximo de energía magnética, es decir, el máximo valor de BxH. A este parámetro (ver area en azul) se le conoce como “Máximo Producto BxH”, o simplemente, (BH)max, y corresponde a una mejor imagen del valor o mérito de un material, en lugar de usar los valores Mr ó Hci por separado. El parámetro (BH)max es el rectángulo de mayor area en el cuadrante II.

Entre los puntos [4] y [5] el material vuelve a ser saturado pero en el sentido opuesto, y de [5] a [6] se retira el campo H y vuelve a quedar con un valor remanente negativo (-Mr), opuesto a mostrado en el punto [3]. Si se aplica un campo nuevamente en el sentido original, de [6] a [7], la magnetización M evoluciona hasta que en [2] se cierra el ciclo de histéresis, donde el material vuelve a estar magnéticamente saturado.

Esta curva de histéresis es equivalente a graficar el campo magnético inducido B, en función del campo magnético aplicado H, es decir, B(H). Así también se obtienen los valores para la Remanencia, Coercitividad y (BH)max.

Un área dentro del ciclo B(H) representa la densidad de energía magnética (J/m3) disipada en forma de calor por unidad de volumen de material. Este calor se debe a la fricción entre los dominios magnéticos.

El área completa encerrada por el ciclo B(H) ó M(H) representa la densidad de energía magnética disipada por unidad de volumen y por ciclo. Mientras mayor sea el área del ciclo de histéresis, “mejor” será el material como imán, y “peor” será como núcleo de transformador.

Cuando un imán opera a temperaturas bajas con respecto a su Temperatura de Curie (Tc), debido al ordenamiento magnético, el imán ferromagnético o la cerámica ferrimagnética operará perfectamente. Sin embargo, si la temperatura aumenta y se tiende a acercar a Tc, todos lo parámetros antes explicados, como Ms, Mr, Hci, (BH)max y el Area del Ciclo de Histéresis serán menores, ya que se produce un desorden magnético por activación térmica. Cuando el material en cuestión alcanza la Tc, el área del Ciclo de Histéresis y el (BH)max son nulas y material, por tanto, pierde toda su remanencia. Por eso, un imán será mejor y rendirá bien cuanto más alta sea su Temperatura de Curie, Tc.

A continuación, y como referencia, se incluyen 5 tipos de materiales con sus respectivos parámetros Br, Hci, (BH)max, entre otros:

http://www.neodymium-magnets-uk.com/magnetic_theory.html

CONCLUSIONES

Por todo lo anteriormente expuesto, creemos sería de gran utilidad calcular, para varias muestras metálicas de Veas-01, los Ciclos completos de Histéresis y determinar empiricamente los parámetros Tc, Mr, Hci, (BH)max y la Densidad de Energía Magnética disipada por unidad de volumen y por ciclo. De esta manera podremos conocer si el material superficial de Veas-01 es un Buen Imán, o bien, si se trata de un Buen Nucleo de Transformador.

¿Cuánto será su (BH)max/USD en el mercado?

Es de esperar que, más bien antes que después, sea posible responder a esta interesante pregunta.

¿Qué edad tiene Veas-01?

LA EDAD DEL UNIVERSO

Nuestro Universo no es estático, sino evidentemente dinámico, y a medida que el tiempo transcurre, todo el Universo conocido se expande de modo tal que si se mide la distancia que separa dos galaxias cualesquiera, ésta aumenta en el tiempo.

Cuando dos galaxias están más próximas entre sí la velocidad relativa de separación es menor, mientras que mayor será esta velocidad cuanto más alejadas estén ambas galaxias. Así entonces, una galaxia distante de nosotros 1 millón de años-luz se alejará de nosotros con una velocidad relativa de 15 a 30 kilómetros por segundo. Una galaxia a 2 millones de años-luz se alejará de nosotros con el doble de la velocidad antes dada, y así sucesivamente.

Edwin Hubble observó este hecho y determinó la constante de proporcionalidad H0, que lleva su nombre, y se escribe en la siguiente expresión:

VELOCIDAD = H0 x DISTANCIA

Usando la estrellas variables conocidas como Cefeidas, es posible establecer una escala para las distancias en el Universo. A pesar que todo el tiempo los astrónomos recalculan la constante H0, un análisis muy simplificado revela que el tiempo T desde “radio cero” hasta la edad actual del Universo, corresponde al inverso de dicha constante H0:

H0 = 15 (kms/s) por millón de años-luz

H0 = 1/(20 mil millones de años) = T del Universo

En otras palabras, la edad máxima del Universo bordearía los 20.000 millones de años.

En referencia al Sistema Solar, la edad que se le calcula al Sol, por ejemplo, se acerca a los 5.000 millones de años, en tanto a nuestra Tierra se le calcula unos 4.500 millones de años.

EDAD DE VEAS-01

Por otro lado, y en relación al tema que nos compete como es la investigación de Veas-01, se ha recibido numerosos correos electrónicos consultando por una posible edad de la Piedra, o solicitando que determinemos, por ejemplo, si ésta es Pre-Solar o no. Así fue que, a fines de 2004, se intentó contestar a esta pregunta analizando la edad de los circones presentes en el interior del metal. Los resultados nunca nos fueron entregados desde Alemania por lo que no nos ha sido posible determinar con mediana precisión la edad física del metal que constituye la Roca Veas-01.

Sin embargo, y a modo de muestra que intentos de estimar una edad se han practicado, durante una conversación en compañía de un buen café post almuerzo, el Dr. Mauricio Belmar sugirió la posiblidad de establecer una edad aproximada de la edad de Veas-01 usando las concentraciones de Uranio (U), Torio (Th) y de Plomo (Pb) determinadas tanto en la matriz metálica como también en las “burbujas” (durante el proceso de perforación y extracción de un cilindro de 10 cms de longitud efectuado meses atrás). El Dr. Belmar mencionó esta opción en base a la posibilidad que presentaba la Microsonda SEM de calcular una edad estimativa de un material midiendo la aparición de estos tres elementos, y siempre que no arrojaran valores dados como Límite de Detección, por el instrumento.

Fue así como el polvo (Muestra A) recogido durante la perforación del cilindro (ver foto arriba) fue enviado al laboratorio Acme Analytical Laboratories Ltd., en Vancouver, Canadá, para un análisis químico multielemental y de trazas, obteniéndose 0.8 ppm de Uranio, 3.1 ppm de Torio y 49.91 ppm de Plomo. Este resultado no entrega una diferenciación de la abundancia isotópica para el Plomo de modo de compararlas con la abundancia terrestre del Pb.

Por otro lado, y usando un laboratorio distinto del de Acme, se procedió a efectuar un análisis multielemental en un trozo (Muestra B) que sólo contuviese metal, sin “burbujas” ni “orificios” macroscópicos, con el objetivo de analizar por ICP de masa el contenido, en ppm, de los tres elementos U, Th y Pb.

El resultado de los análisis reflejaron una cantidad parecida para el U y Th obtenidas por Acme Laboratories pero una diferencia sustancial para el plomo: 1.0 ppm de Uranio, 3.0 ppm de Th, y 276 ppm de Pb. Tampoco el informe entrega la abundancia isotópica del Pb.

No obstante, si suponemos que la abundancia isotópica del plomo en Veas-01 es similar al terrestre, entonces deberemos diferenciar los cuatro isótopos naturales de este elemento Pb antes de usar las ecuaciones para la ley de decaimiento radiactivo, y por tanto, antes de calcular la edad del material que compone la Roca.

El Plomo terrestre (Pb) posee aproximadamente un 1.48% de Pb-204, un 23.6% de Pb-206, un 22.6% de Pb-207 y un 52.3% de Pb-208. Ahora bien, el Pb-204 es estable y no posee precursores radiactivos naturales, en tanto que el Pb-206 y Pb-207 provienen del U-238 y U-235, respectivamente. Por último, el Pb-208 tiene como precursor radiactivo primario al Th-232. Aunque el Th-232 decae temporalmente en otros subelementos antes de formar Pb-208, podemos estimar la Semi-Vida (t/2) entre ambos elementos en 14.100 millones de años.

Para los datos proporcionados por ACME Analytical Laboratories (Muestra A), y suponiendo una abundancia isotópica terrestre para el plomo, de los 49.91 ppm de Pb, sólo 26.10 ppm corresponderían a Pb-208, en tanto para los datos dados por el segundo laboratorio, de los 276 ppm de Pb, sólo 144.35 ppm serían de Pb-208. Para ambos casos, se ha supuesto razonablemente que todos los ppm de Pb-208 acualmente detectados, en un comienzo pertenecían a átomos (o ppm) de Torio. Esto significaría que la Muestra A tenía hace varios millones de años la cantidad de 29.2 ppm de Th, en tanto la Muestra B poseía la cantidad de 147.35 ppm de Th-232.

Si Af es la cantidad (en ppm) final de Th en la muestra, A0 es la cantidad inicial (en ppm), y conociendo la Semi Vida del Th-232, y haciendo uso de la ecuación:

Edad (en años) = (t/2) x Ln (Af/Ao)

resulta, entonces, para la Muestra A, en una edad aproximada de 45.600 millones de años, en tanto para la Muestra B, en una edad del orden de 79.311 millones de años.

DISCUSION DE LOS RESULTADOS

Si observamos estas edades calculadas para la Muestra A y Muestra B, vemos que éstas superan, respectivamente, los 2.28 y 3.96 veces la edad del Universo Conocido, calculado por medio de la Constante de Hubble, Ho; por lo cual, en principio (y debido al hecho que experimentos más sensibles son requeridos) estas dos edades, calculadas para el metal de Veas-01, serán descartadas de plano.

Por lo anterior, y como una forma de comprobar en forma sistemática una posible edad confiable para Veas-01 usando los contenidos de U, Th y Pb, se necesitará:

1.- Un instrumento que pueda medir hasta en una parte por trillón (ppt) como Límite de Detección, permitiendo valores confiables para las concentraciones de U, Th y Pb.

2.- Un equipo sensible, como un ICP-Masa, que permita “separar” del plomo sus cuatro isótopos naturales como lo son Pb-204, Pb-206, Pb-207 y Pb-208, y comparar sus abundancias con las terrestres. Idem, para el Uranio con sus isótopos U-235 y U-238.

3.- Un laboratorio confiable que pueda efectuar y certificar la edad de los Cristales de Circón presentes en la matriz de fierro de Veas-01.

Sólo mediante un riguroso procedimiento científico, y usando modernos equipos de avanzada tecnología, como por ejemplo, el Ciclotrón que posee la Comisión Chilena de Energía Nuclear (adquirido con fondos de todos los chilenos), podremos determinar y publicar de modo confiable y seguro una posible edad para Veas-01.