AGUA METALICA

En los artículos anteriores, y en referencia al estudio de la Gran Roca Metálica denominada Veas-01, hemos revisado brevemente modelos que simulan las posibles estructuras cristalinas adoptadas por átomos de Fe cuando éstos han sido sometidos a alta temperatura y presión.

En efecto, en el artículo sobre la Hexagonal Close-Packed para el Fe, se mencionaban modelos que postulaban temperaturas del orden de 7000 ºK y presiones variables entre 100 y 350 GPa.

Nuestros últimos comentarios en este Blog han sido dirigidos a pensar en diferentes Radios Iónicos para los átomos de Fe presentes en una estructura formada a alta presión, diferenciándose totalmente de los átomos de Fe formados a presión ambiental, dificultando entonces la interpretación de los patrones de difracción observados con el TEM (sin considerar los efectos magnéticos de las muestras). Ahora bien, si los Radios Iónicos para los átomos de Fe están alterados, son distintos entre sí, y a su vez, diferentes al Radio Atómico Calculado de 1.56 Angstroms, es probable también que la densidad electrónica de un estado electrónico parcialmente ocupado, responsable de la conductividad, también está alterado. En definitiva, este grado de alteración y de desorden de la “nube electrónica” puede ser responsable del rechazo de zonas a los electrones de 200 keV provenientes del filamento de tungsteno del TEM, pues el enlace metálico implica que los electrones no están fuertemente ligados a los núcleos atómicos del material correspondiente.

Lo anterior, por otro lado, lleva a pensar que probablemente el metal que constituye Veas-01 sufrió una fuerte y violenta explosión, además de las altas presiones y temperaturas implicadas en su formación. Esto promueve el planteamiento de dos hechos quizá sucedidos para con Veas-01: (1) primero la formación de una estructura cristalina, para los átomos de Fe, generada a una alta temperatura y presión, y (2) una fuerte explosión o estallido de la matriz metálica creó una brusca disminución de la presión y de la temperatura, alterando quizá no sólo la estructura cristalina sino también la conductividad eléctrica y iónica del material, por alteración de la densidad electrónica.

Por ello, imaginémonos las condiciones extremas existentes en el interior de un planeta de grandes dimensiones, en el que escogemos investigar un compuesto, menos denso que el Fe, existente en un planeta también menos denso que el planeta Tierra, como lo es Neptuno. Podemos entonces preguntarnos:

1.- ¿qué sucedería si sometiésemos a altas presiones y temperaturas a un compuesto formado sólo por átomos de H y O, como el agua?.

2.- ¿podríamos pensar que el agua pueda volverse magnética y conductora como un metal, y por tanto suponer, que esta “Agua Metálica” formada a Alta Temperatura y Presión sea responsable, en parte, del Magnetismo de un planeta como Neptuno?.

3.- ¿Implicará, la creación de esta “Agua Metálica” conductora, un proceso de tipo “explosivo” o brusco, donde la presión y la temperatura descienden rápidamente?.

Las respuestas a estas interesantes interrogantes fueron propuestas por los científicos Thomas Mattsson y Mike Desjarlais, ambos investigadores del Laboratorio Sandia, dependiente del National Nuclear Security Administration.

Sandia Laboratory está bajo la dirección de Sandia Corporation, la cual es una empresa Lockheed Martin, operando para el U.S. Department of Energy’s National Nuclear Security Administration. Sandia centra sus objetivos en Investigación y Desarrollo en Seguridad Nacional, y Tecnologías Energéticas y Ambientales.

www.sandia.gov

El “Agua Metálica” bajo Condiciones Extremas

Los investigadores ya mencionados, Thomas Mattsson y Mike Desjarlais, usando supersimuladores han significativamente alterado el diagrama teórico universalmente utilizado por los científicos para entender las características del Agua sometida a presión y temperatura extremas. Por otro lado, este nuevo modelo computacional ha ampliado la comprensión sobre la conductividad eléctrica del agua.

El trabajo teórico llevado a cabo por el Laboratorio Sandia mostró que la fase límite para obtener la fase denominada Agua Metálica, en la cual los electrones del agua pueden migrar como en un metal, se logra al disminuir la temperatura de 7000 a 4000ºK, y la presión desde 250 GPa al valor de 100 GPa.

Recordemos que una fase límite describe las condiciones a la cual un material cambia de estado. Para el caso del agua, que en su estado puro, es un aislador eléctrico, bajo estas condiciones de disminución de T y P, el agua se vuelve un conductor.

Este nueva condición ha determinado que deben revisarse los cálculos de los astrónomos en orden a evaluar la fuerza de los núcleos magnéticos de planetas gaseosos gigantes como lo es Neptuno. Debido a que las presiones y temperaturas de los planetas “caen” parcialmente en el “sector revisado”, el agua electricamente conductora probablemente contribuye a su campo magnético, que antes se pensaba era generado sólo por el núcleo del planeta.

Estos cálculos concuerdan con los resultados experimentales en investigaciones llevadas a cabo por el Dr. Peter Celliers del Lawrence Livermore National Laboratory.

Mattsson y Desjarlais, quienes participan en la implementación de poderoso acelerador de Sandia conocido como Z (que comenzará a funcionar hacia julio de 2007), deseaban tener un mejor entendimiento del agua bajo condiciones extremas. Ellos encontraron que el diagrama de fase estándar del agua quedaba “fuera de rango” cuando “corrían” el programa de simulación molecular cuántico en el supercomputador Thunderbird de Sandia, el cual incluía electrones “calientes” en lugar de los “frios no realísticos”.

El modelo molecular conocido como VASP, basado en la Teoría Funcional de Densidad (DFT), había sido escrito en Austria. Desjarlais extendió VASP para modelar la conductividad eléctrica en tanto Mattsson desarrolló un modelo para la conductividad iónica basada en los cálculos de la Difusión de Hidrógeno. Una descripción rigurosa del agua requiere un tratamiento combinado entre conductividad electrónica y iónica.

Para la adaptación del modelo VASP a lo que Sandia necesitaba, se basaron en los trabajos preliminares de medición de la conductividad en “alambres sometidos a explosión”, desarrollados por Alan DeSilva, de la Universidad de Maryland. DeSilva encontró una considerable disparidad entre sus datos y los modelos teóricos de materiales en la región del espacio de fase conocida como “materia densa caliente”. Los cálculos de conductividad desarrollados por el nuevo VASP de Desjarlais resolvieron inmediatamente esta discrepancia.

La estructura electricamente conductora del Agua Metálica sucede en una parte más accesible del diagrama de fase del agua, de lo que anteriormente se suponía. En la imagen de arriba se observa una instantánea de una simulación de primeros principios demostrando el desorden atómico de la misma. Las esferas rojas son los átomos de Hidrógeno, las esferas blancas son los átomos de Oxígeno, en tanto la densidad electrónica del estado del electrón parcialmente ocupado, responsable de la conductividad, se muestra en dorado.

Este trabajo de las fases del agua fue inicialmente publicado el 7 de julio de 2006 en la Physical Review Letters en tanto resultados fueron expuestos en 12th International Workshop de Fisica de Plasmas No-Ideales, que se llevó a cabo en Darmstadt, Alemania.

SOLO IMAGENES

ANALISIS DE MUESTRA EN TEM

INTRODUCCION

Un par de meses atrás, en este mismo blog, efectuamos una publicación en donde se indicaba, como uno de los objetivos, el obtener la estructura cristalina, o las fases minerales para el Fe puro, presente en muestras metálicas extraídas de la Gran Roca Veas-01. Se analizó también, en dicho artículo, la posibilidad de encontrar la estructura HCP para el Fe, debido a los supuestos que han hecho pensar en altas presiones implicadas en su formación.

Se inició conversaciones con un especialista en el manejo de un Microscopio Electrónico de Transmisión (TEM) de modo de estudiar la posibilidad de someter algunas muestras de Veas-01 al haz de electrones de 200 keV de energía, con una longitud de onda de 0.027 Angstroms para tales electrones, y así determinar los patrones de difracción para los diferentes Ejes de Zona analizados sobre la muestra.

Utilizando el cilindro de aproximadamente 9 cms de longitud, extraido desde la superficie de Veas-01 meses antes por los geólogos e investigadores César Arriagada y Brian Townley, se procedió a obtener una delgada lámina del diámetro de una moneda continuando con los siguientes procesos:

1.- Pulido y rebaje del espesor de dicha lámina metálica hasta un valor próximo a las 280 micras.

2.- Corte de muestras circulares, desde la lámina, de sólo 3 mm de diámetro, obteniéndose de esta forma más de 4 muestras de 1.5 mm de radio y 280 micras de espesor.

3.- Posterior rebaje central de cada una de las diminutas muestras mediante un esmeril micrométrico hasta que obtener alrededor de 5 micras de espesor justo al centro de cada una de las muestras.

4.- Cada una de las pequeñas muestras, luego del paso anterior, deben ser sometidas a un Ion Milling (Rebajador Iónico), de tal forma que un haz de iones de Ar(+) terminen de rebajar el área central de cada muestra hasta “abrir” zonas, permitiendo obtener delgadas zonas de material posibles de ser “traspasadas” por el haz de electrones del TEM.

5.- La muestra ya rebajada está lista para ser analizada por el TEM.

MUESTRA DE VEAS-01 EN UN TEM

Habiéndose cumplido todos los pasos antes descritos, se procedió a ingresar una muestra de la Roca Metálica al Microscopio Electrónico de Transmisión. Luego de tomar una serie de microfotografías de rigor, el trabajo consistió en estudiar una delgada zona de una micra de diámetro, “transparente” al haz de electrones. .

Una de las primeras observaciones interesantes de notar fue el magnetismo que la pequeña muestra ejercía sobre el haz de electrones de 200 keV, generando efectos de “torsión”, astigmatismo y rechazo del haz de acuerdo con la zona donde se el haz se posicionaba.

Dentro de esta area de tan sólo una micra de diámetro pudo observarse Ejes de Zona que “torsionaban” el haz, en tanto otros Ejes de Zona literalmente rechazaban el haz impidiendo su estudio o fotografía.

Dejando fuera los Ejes de Zona que nunca pudieron ser analizados, porque rechazaban el haz, y considerando sólo aquellos que permitieron su observación, es importante exponer que nunca fue posible corregir el astigmatismo que la muestra producía sobre el haz. Se calibraba y corregían todos los parámetros del haz sobre el plano de observación (lejos de la influencia de la muestra de Veas-01), pero al acercar el metal al haz, la muestra provocaba inmediatamente un fuerte astigmatismo al haz de electrones, el cual nunca pudo ser removido, de modo que todos los patrones de difracción que pudieron obtenerse corresponden a haces con fuerte astigmatismo.

La literatura técnica sobre Microscopía Electrónica de Transmisión dice que el astigmatismo aparece cuando los electrones encuentran un campo magnético B no completamente uniforme, distorsionando la imagen. Este efecto se debe a la presencia de Piezas Polares, aperturas en las lentes, contaminación, etc. En otras palabras, cuando el lente tiene diferentes distancias focales, dependiendo del plano de viaje de los electrones, se produce el Astigmatismo, lo cual directamente deteriora la resolución del TEM. La falta de simetría rotacional del campo hace que aparezca este tipo de defecto, haciendo que la imagen astigmática se muestre alargada hacia una dirección.

En nuestro caso, se tomaron los patrones de difracción sin corregir ni evaluar el astigmatismo que la muestra metálica de Veas-01 provocaba sobre el haz, lo cual actualmente estamos analizando, para extraer conclusiones a partir de los pocos patrones de difracción obtenidos (de los escasos ejes de zona que pudieron ser analizados) por causa del mencionado efecto de rechazo al haz mostrado por los restantes ejes de zona.

Así por ejemplo, para hacer la corrección y evaluar el astigmatismo del lente objetivo del TEM se hace uso de las Franjas de Fresnel que se forman en un hueco en una membrada de Colodión. Considerando la longitud de onda de los electrones, y el Espesor Máximo y Mínimo de la Franja de Fresnel, es posible evaluar el Astigmatismo Residual.

El efecto de torsión, que tenía lugar como una consecuencia del magnetismo propio de la muestra, presentaba imágenes como el dibujo que se indica a continuación:

A pesar de los problemas, hubo ejes de zona donde pudieron obtenerse imágenes como la siguiente:

la cual es un patrón típico de las formas hexagonales, como por ejemplo, para la Hexagonal Close-Packed ó HCP.

No obstante, como no nos ha sido posible obtener todos los patrones de difracción correspondientes a la mencionada zona de tal sólo 1 micra de diámetro, y debido al hecho que es necesario “escudriñar” otras zonas dentro de la misma muestra, además de las muestras restantes ya pulidas y rebajadas, no nos parece serio ni científico el aventurar conclusiones erróneas sin primero considerar las correcciones antes descritas, además de aumentar el número de las mediciones para obtener un universo estadístico confiable.

Además de los efectos ya descritos, que deben mejorarse y calcularse para futuros análisis, los especialistas en Microscopía Electrónica de Transmisión entregan un par de consideraciones adicionales que deben tenerse en cuenta respecto de análisis con TEM:

1.- la información obtenida es muy local, debido al hecho que se evalúa sólo una porción muy pequeña del material. El TEM debe, por ello, emplearse después de otras técnicas de caracterización microestructural que permitan cierta “perspectiva”.

2.- Está el problema de tener que evaluar una imagen bidimensional con información tridimensional.

Por ejemplo, en esta imagen aparecen dos rinocerontes en perpectiva, pero que en una proyección bidimensional semeja ser una sóla bestia de dos cabezas. Aunque este tipo de imágnes son fácilmente diferenciables para el ojo humano, no lo es para instrumentos como el TEM, donde pueden producirse mal interpretaciones a partir de características “reales”.

CONSIDERACIONES CRISTALOGRAFICAS

Desde el punto de vista de la segunda consideración técnica antes mencionada, esto es, saber extraer información tridimensional a partir de imágenes bidimensionales, daremos una breve mirada del cómo efectuar correcta interpretación a partir de los patrones de difracción adquiridos por un TEM (suponiendo cristales que no poseen un magnetismo tan intenso como para afectar el haz de electrones).

Supongamos que tenemos un gas encerrado a temperatura constante. Las moléculas de ese gas ejercerán una presión como consecuencia de los choques entre ellas y las paredes de la cámara que las contiene. Estas moléculas se moverán con una velocidad proporcional a la temperatura del ambiente que las rodea. A medida que sacamos moléculas de la cámara la presión disminuirá, de modo que la presión es función de la densidad del moléculas. A medida que la densidad disminuye, el camino libre medio recorrido (distancia recorrida por una partícula entre dos choques sucesivos) por las partículas será mayor.

Para el caso del aire, a presión atmosférica, las moléculas tienen un camino libre medio de 70 nm aproximadamente, valor que mejora a 7 mm cuando la presión disminuye a 0.01 mbar. Para el caso de un TEM, los electrones deberán recorrer “metros” sin ningún choque con moléculas, desde su orígen hasta impactar la muestra. Este efecto se logra con presiones por debajo de los 10E(-5) mbar.

Resuelto el problema del vacío, debemos considerar lo que sucede cuando el haz de electrones golpea los centros o núcleos atómicos que componen la muestra a analizar. Los núcleos de los átomos se comportan, entonces, como “rejillas de difracción” de modo que el resultado de la imagen difractada es un patrón de puntos bastante diferente del que posee el cristal real que compone la muestra. A cada centro atómico (sin su nube de electrones) se asigna un punto, de manera que al conjunto de puntos que forma la red del cristal real se le conoce como Red Directa. En tanto, al conjunto de puntos que forma el patrón de difracción (imagen del cristal real) se le denomina Red Recíproca.

Lo anterior significa que debemos ser muy cuidadosos al interpretar algo que sucede en la Red Recíproca como que estuviese sucediendo en la Red Directa. La Red Recíproca es, en efecto, la Transformada de Fourier de la Red Directa.

Para dar un ejemplo, consideremos una muestra de Oro Puro, que es usado como una muestra patrón para efectos de calibración. El Au puro posee una estructura cristalina tipo FCC, con una distancia entre núcleos atómicos de 2.884 (A). Si suponemos que todos los átomos de Au tienen un mismo radio iónico, éste será entonces, la mitad del valor dado anteriormente, es decir, 2.882/2 = 1.442 Angstroms.

¿Cómo se verá el cristal del Au en la Red Recíproca, luego que el haz de electrones impacte la Red Directa?.

Como veremos luego, los vectores unitarios de una fase FCC formarán ángulos entre sí de 60º, en tanto los vectores unitarios de una estructura BCC formarán ángulos de 70.53º entre ellos.

Lo anterior implica que, cristales de oro FCC con parámetro “a” de 2.884 (A) se verán en la Red Recíproca como un cristal de estructura BCC con parámetro de red “a” = 0.60 Angstroms, de modo tal que todos los patrones de difracción que obtenga con el TEM serán los típicos de una red cúbica BCC. En otras palabras, el Au será efectivamente una forma BCC pero sólo en la Red Recíproca, puesto que la Transformada de Fourier de una forma FCC será una estructura BCC.

A diferencia, si el Au fuese una estructura BCC en la Red Directa de parámetro “a” igual a 2.884 (A), en la Red Recíproca se vería una fase FCC de parámetro “a” igual a 0.49 (A) en vez de los 0.60 (A) del caso anterior. No obstante, y como ya se explicó anteriormente, el Au cristaliza unicamente como FCC.

Si tomamos, como ejemplo de una estructura BCC, el cristal de Tungsteno, y suponiendo que todos sus átomos tienen el mismo Radio Iónico (en este caso, igual al Radio Atómico) de 1.371 (A), el parámetro de la red “a” será de 2.742 (A).

Para el Tungsteno, entonces, el cristal en la Red Recíproca se verá como una forma FCC de parámetro “a” igual a 0.516 (A), siendo todos sus patrones correspondientes a aquellos de una forma FCC, con la salvedad que no debemos olvidar que estamos trabajando en la Red Recíproca, que es la que en definitiva, nos entrega el instrumento, en este caso, el TEM.

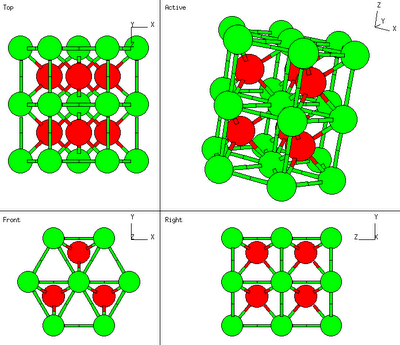
REDES CUBICAS

La figura anterior nos entrega además de la forma, de las principales redes cúbicas, los correspondientes vectores unitarios en la Red Directa.

Otras características de las tres celdas cúbicas son dadas a continuación en la siguiente tabla:

Efectuemos ahora un cálculo para demostrar lo que sucede al calcular los vectores unitarios de una Red Recíproca cuando en la Red Directa tenemos ya sea una forma BCC o una FCC.

En el siguiente ejemplo se muestra cómo los vectores unitarios de una estructura BCC se transforman, en la Red Recíproca, en los vectores unitarios de una forma FCC.

En el segundo ejemplo, que damos a continuación, mostramos cómo a partir de vectores unitarios de una forma FCC llegamos a obtener, en la Red Recíproca, vectores unitarios de una forma BCC.

De ambos ejemplos podemos notar que los vectores unitarios de una forma BCC forman ángulos de 70.53º entre ellos, en tanto para las formas FCC los ángulos formados entre sus vectores son de 60º.

Evidentemente, y no es necesario efectuar un cálculo mayor, la Red Recíproca de una forma cúbica simple será también un Cubica Simple de parámetro igual al inverso de a multiplicado por una constante, como puede ser 2pi.

LA RED RECIPROCA DE UNA FORMA HCP-Fe

Regresemos ahora al tema de la estructura HCP para el Fe, la cual se cree puede formar los núcleos de planetas de tamaños superior o similares al nuestro. De acuerdo con los cálculos efectuados en la Universidad de Bayreuth por el Dr. Gerd Steinle-Neumann, las presiones involucradas en la formación de la HCP para el hierro pueden alcanzar hasta los 350 GPa. Dependiendo del rango de presiones, entre los 200 y los 350 GPa, también existirá una variación de las distancias interatómicas entre los átomos de Fe tanto en el plano a-b como en el eje c.

Recordemos que una presión de un Pascal equivale a 9.8 E(-6) atmósferas, de modo que 350 GPa equivalen a 3.430.000 atmósferas (casi 3 millones y medio de atmósferas terrestres). A esta presión es posible que los Radios Atómicos para el Fe sean diferentes dentro de un mismo cristal, con Radios Ionicos posiblemente también distintos.

La molécula del óxido de fierro conocido como Magnetita (descrito en nuestro artículo anterior) posee tres átomos de Fe con dos estados de oxidación, II y III, implicando la presencia de 2 átomos Fe(+3) y 1 átomo de Fe(+2). Esto significa que la Magnetita tendrá dos átomos de Fe con Radio Ionico de 0.64 Angstroms y un átomo de Fe con Radio Iónico de 0.76 Angstroms. Estos valores contrastan con el Radio Atómico del Fe neutro de 1.56 Angstroms que podemos encontrar aproximadamente para los átomos de Fe dentro de una forma BCC o FCC a la presión ambiental de sólo una atmósfera.

Por lo anterior, y considerando las grandes presiones de más de 3 millones de atmósferas que presuntamente darían orígen a formas HCP-Fe en los núcleos de planetas, sería poco probable encontrar el que todos los átomos de Fe tuviesen radio normal, alterando entonces la razón c/a para una HCP de entre 1.6 a 1.633. De la tabla entregada por el Dr. Gerd Steinle-Neumann, y publicada en este Blog, podemos observar que para presiones en torno a los 200 GPa, la razón c/a será de 2.18/2.21 igual a 0.9864. Para presiones en torno a los 250 GPa la razón c/a será de 2.13/2.16, igual a 0.9861, en tanto para presiones del orden de los 350 GPa la razón c/a será de 2.08/2.12 igual a 0.9811. Esto implica que, a muy altas presiones, la altura del eje c será casi numericamente igual al valor de los vectores a y b en el plano de la Hexagonal Close-Packed (HCP). Como evidentemente esto no tendría sentido si todos los átomos de Fe tuviesen el mismo radio, es de suponer que existirán planos dentro del cristal con radios iónicos distintos entre sí.

De igual forma que efectuamos los cálculos para la formas BCC y FCC en la Red Recíproca, podemos hacer lo mismo para una estructura HCP. Así entonces, una forma HCP en la Red Directa se verá también como una HCP en la Red Recíproca, tal como se esquematiza en el siguiente diagrama que compara la forma hexagonal con las formas cúbicas.

De la figura anterior podemos notar que la celda unitaria de una HCP tendrá un átomo centrado en el cuerpo, como en el caso de la BCC. Como el ángulo entre los vectores a(1) y a(2) serán de 120º entre sí, o bien de 60º según dónde se sitúe el orígen, y la razón c/a será de 1.633, la celda unitaria de una forma HCP será fácilmente diferenciable de una forma BCC.

Más, ¿qué sucede con la visualización de una HCP cuando los Radios Iónicos de sus cristales son diferentes entre sí?.

Sólo por hacer un cálculo extremo, supongamos una presión tal elevada, de unas 4 millones de veces la atmósfera terrestre, que la razón entre el eje c y los vectores planares entreguen el valor c/a de 0.8696, en vez de 0.98, determinadas por el Dr. Gerd Steinle-Neumann. Esta suposición implicará que aunque los vectores c y a sean numéricamente diferentes en la Red Directa, éstos no lo serán en la Red Recíproca. En efecto, si calculamos la HCP resultante en la Red Recíproca, nos encontraremos con que los tres vectores a(1), a(2) y a(3) tendrán el mismo módulo o longitud. Más, aún podemos diferenciar las celdas unitarias HCP de la BCC por el ángulo de 60º formado entre los vectores recíprocos a(1)* y a(2)* de la HCP comparado con los 90º formados entre los vectores base de una BCC (ver figura siguiente).

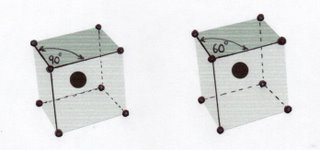
Para que no “quepa lugar a dudas” que la Red Recíproca de una forma HCP es también una HCP, consideremos la siguiente demostración de la transformación de los Vectores Unitarios de la Red Directa hacia la Red Recíproca.

En este cálculo anterior se observa claramente que la HCP de la Red Recíproca está girada 30º con respecto a la HCP que el cristal posee en la Red Directa.

Consideremos ahora el supuesto de c/a igual a 0.8696 para una HCP formada por átomos de Fe de diferentes Radio Ionicos, de modo que se cumpla esta condición dada entre el eje c y los vectores planares. Si imaginamos un módulo de 2.12 angstroms para los vectores a y b en el plano de la Hexagonal Close-Packed, el vector a(3) o vector c tendrá una longitud de 1.84 angstroms.

Sin embargo, en el espacio de la Red Recíproca los tres vectores tendrán la misma longitud de 0.94 Angstroms, en tanto los vectores a(1)* y a(2)* formarán un ángulo de 60º entre sí. De esta manera la celda unitaria de esta HCP en la red Recíproca se verá como una Celda BCC "deformada" en el plano basal (debido a que se trata en verdad de una HCP, con lados a = b = c), donde los vectores basales no formarán 90º sino esta vez 60º.

CONCLUSIONES

De todo lo anteriormente explicado, y en relación a la Roca Veas-01, podemos concluir lo siguiente:

1.- Aunque algunos especialistas creen que el magnetismo propio de las muestras de Veas-01 corresponden a un fenómeno magnético observado en otras muestras metálicas, ellos no han podido sugerir cómo corregir el fenómeno del astigmatismo sucedido con el haz de electrones del TEM, de 200 keV de energía, como tampoco han podido indicar o sugerir muestras materiales conocidas que muestren un comportamiento tan interesante como el de “rechazar” literalmente el haz de electrones por parte de ciertos Ejes de Zona, impidiendo la observación de dicha área.

2.- Si suponemos altas presiones en la formación del material metálico que constituye Veas-01, podemos pensar que el hecho que, dentro de tan sólo una micra hayan efectos de rechazo del haz, torsión del haz y astigmatismo del mismo, implica una disposición de átomos de Fe con diferentes Radios Iónicos involucrados, como sucede con la Magnetita, que es también magnética. Aunque los patrones de difracción nos entrega figuras planas representativas de la distancia entre centros atómicos, mientras no conozcamos cuántos estados de oxidación están presentes en estos cristales de Fe, nuestros resultados no pueden ser concluyentes. Y el Fe posee seis estados de Oxidación. En efecto, si existen ciertos ejes de zona, dentro de tan sólo una micra de diámetro, que rechazan el haz de electrones de carga negativa, implica que el mencionado eje de zona debe tener una gran nube de electrones ligada fuertemente a una zona altamente positiva, haciendo la diferencia con los enlaces metálicos usuales. Además, el hecho que estos Ejes de Zona rechacen el haz de electrones de energía 200 keV, nos dice mucho sobre el orden de magnitud de la energía presente en torno a esta área.

3.- El estado de oxidación Fe(VI) supuestamente es Anfótero (ver artículo antrerior), de modo que los resultados que puedan entregar las pruebas de PH efectuadas por el Dr. Brian Townley sobre la superficie metálica de Veas-01, será un test interesante para conocer si Veas-01 reacciona como una base en un medio ácido, o bien como un ácido en un medio básico, contrarrestando el PH del medio. ¿Qué valor para el Radio Iónico tiene el Fe(6+)?.

4.- Tal como lo muestran los modelos de HCP calculados por la Universidad de Bayreuth, las razones entre las distancias c/a en la Red Recíproca son cercanas a la unidad, de modo que patrones de difracción, tanto cúbicos como hexagonales, podrían ser hallados con Microscopia Electrónica de Transmisión (TEM), como sucedió con los análisis efectudos con una muestra de Veas-01.

5.- Nos obstante, como no fue posible corregir los efectos de astigmatismo del haz del TEM, por causa del fuerte magnetismo emanado de la muestra, y debido a que este hecho disminuye fuertemente la resolución del TEM, creemos no confiable publicar las imágenes obtenidas, porque aunque aparecieron patrones tanto hexagonales como algunos cúbicos (indicativos quizá de una Hexagonal Close-Packed de alta presión), debemos conocer bien cómo corregir las anomalías del haz sobre la muestra antes de efectuar pruebas confiables. Algunos especialistas propusieron hace décadas que, para muestras HCP-Co magnéticas, era conveniente calentarlas hasta el punto donde el magnetismo decreciera, antes de introducirlas al TEM. Para nuestro caso, sabemos que se requerirá de al menos 700ºC para quizá conseguir una disminución del magnetismo, aunque no estamos seguros de ésto porque no ha sido posible encontrar un horno que mida la Temperatura de Curie Tc de las muestras de Veas-01.

6.- Aunque no fue posible conocer con precisión todos los patrones de difracción de la muestra de Veas-01 puesta en el TEM, los fenómenos de astigmatismo, torsión y rechazo ocurridos para con el haz de electrones descartan, en principio, una estructura BCC ó FCC para el material de Veas-01, ó al menos descarta estas formas con Radios Atómicos iguales para los átomos de Fe. La fuerte resitencia de la muestras a la alta temperatura, sin decrecer su magnetismo, el magnetismo propio de la Roca Veas-01, como un todo, el magnetismo propio e intenso de las muestras diminutas ante la presencia del haz de electrones creando efectos de torsión, rechazo y astigmatismo, sumado al gran y descomunal tamaño de Austenita, más inclusiones como el (Fe,Mn)S indicativas de una alta presión de formación, todos estos detalles vaticinan una estructura totalmente diferente de las conocidas hasta el momento.

7.- El hecho que una zona o área tan pequeña como una micra, dentro de una muestra de 3 mm de diámetro y espesor variable entre 50 y 3 micras, pueda astigmatizar un haz de electrones, o desviarlos o torsionarlos, implica que la estructura cristalina tiene una conformación totalmente diferente a una BCC o FCC formada en los aceros a presión normal, lo cual se sumaría a los experimentos realizados con Prompt-Gamma en el Reactor Nuclear de la Reina; resultados publicados anteriormente en este Blog.

Fases Minerales en Sideritos

INTRODUCCION

Aunque especialistas en meteoritos como el Dr. Michael Zolensky del Johnson Space Center de NASA, en Estados Unidos, sostienen que los meteoritos metálicos poseen estructuras cristalinas amorfas, lo cual dificultaría la identificación de fases minerales, nuestro equipo científico piensa que, a la luz de los conocimientos que hoy se tienen de las estructuras minerales presentes en la matriz de los sideritos, es posible en gran medida identificar los tipos de fases que son posibles de hallar en estos cuerpos metálicos extraterrestres, trátese éstos de Hexahedrites, Octahedrites o bien de Ataxites. Estas últimas tres grandes clases son identificables según el porcentaje de Ni presente en el siderito en particular (ver clasificación en primeros artículos publicados en este Blog).

Si bien compuestos diversos pueden ser encontrados en los meteoritos metálicos, el presente artículo se centrará brevemente en las estructuras cristalinas que son observadas tanto en el Fe puro presente en los sideritos como en las fases formadas entre los elementos Fe y Ni.

Fases formadas por Fe puro y Fe y Ni

Considerando algunos de los compuestos minerales que son posibles de hallar en cualquier meteorito metálico podemos describir los siguientes:

I.- Kamacita: conocida como la alfa-(Fe, Ni), posee un peso molecular de 56.13 gramos, de fórmula empírica Fe(0.9)Ni(0.1), y cuyos átomos de Fe no son oxidados, es decir, que poseen un radio atómico calculado de 1.56 (A). Considerando la composición química de esta fase tenemos que la Kamacita presenta un 89.54% de Fe y un 10.46% de Ni.

Desde el punto de vista cristalográfico, la Kamacita pertenece al Grupo Espacial F m3m, con simbolo de Hermann-Maugin (H-M) 4/m -3 2/m, que corresponde a la Clase Isométrica – Hexoctaédrica.

Las dimensiones de la celda son: “a” = 8.603 (Angstrom), Z = 54, Volumen = 636.7 (Angs 3), y densidad de 7.90 (grs/cm3).

II.- Taenita: se reconoce también como gamma-(Fe,Ni), posee un peso molecular de 56.42 gramos, con una fórmula empírica de Fe(0.8)Ni(0.2), no presentando estados de oxidación los átomos de Fe, esto es, sus átomos son Fe(0+). En cuanto a la composición quimica, la Taenita presenta un 79.19% de Fe y un 20.81% de Ni.

Desde el punto de vista cristalográfico, y al igual que la Kamacita, la fase mineral Taenita pertenece al Grupo Espacial F m3m, con simbolo de Hermann-Maugin (H-M) 4/m -3 2/m, que corresponde a la Clase Isométrica – Hexoctaédrica.

Las dimensiones de la celda son: “a” = 3.596 (Angstrom), Z = 4, Volumen = 46.5 (Angs 3), y densidad de 8.06 (grs/cm3).

III.- Fe puro: El hierro puro presente en los meteoritos metálicos, aunque es cúbica, no posee empero la típica forma BCC ni FCC que adopta normalmente el Fe trabajado. El peso molecular es de 55.85 gramos, y además de haber sido hallado en sideritos, o en trozos de asteroides, este Fe(0+) puro raramente ha sido encontrado en algunos basaltos en paises como Alemania y Grecia. Los átomos de este Fe puro son no oxidados, es decir, del tipo Fe(0+).

Desde el punto de vista cristalográfico este Fe puro presente en los sideritos pertenece al Grupo Espacial I m3m, con simbolo de Hermann-Maugin (H-M) 4/m -3 2/m, que corresponde, al igual que los minerales Kamacita y Taenita antes descritos, a la Clase Isométrica – Hexoctaédrica, cuya estructura cristalina se muestra a continuación:

Las dimensiones de la célda cúbica del Fe meteorítico es de “a” = 2.874 (A), Z = 2, Volumen de 23.74 (angstrom cúbicos) y densidad calculada aproximada de 7.81 (grs/cm3).

Algunos otros datos sobre la estructura Hexoctaédrica son:

Para más información de consulta, por favor, visite el siguiente sitio web:

http://webmineral.com/data/Iron.shtml

Estados Oxidados del Fe

Por definición, el Radio Atómico Calculado de un átomo cualquiera está dado por la configuración electrónica de sus capas de electrones, calculándose como la distancia que existe entre el núcleo del átomo y el electrón de valencia más externo o alejado del nucleo.

El enlace metálico es el responsable de mantener unidos los átomos del metal entre sí. Los enlaces metálicos hacen que los átomos de un metal específico adquieran estructuras típicas de empaquetamiento compacto de esferas.

Los metales poseen una baja electronegatividad, de modo que los electrones de valencia son extraidos de sus órbitas más externas, permitiendo que éstos se muevan libremente a través del compuesto o monocristal metálico, déndoles propiedades eléctricas y térmicas a dichos metales.

Otra característica de los metales como en el caso del Fe es el conocido fenómeno del Efecto Fotoeléctrico, donde los átomos del metal tienden a perder los electrones de las últimas capas cuando dichos átomos reciben fotones o cuantos de luz de una longitud de onda específica.

El Fe(0+) corresponde al átomo de este elemento cuando no presenta estado oxidado alguno, es decir, cuando su configuración electrónica está completa: [Ar]3d(6) 4s(2), implicando que su Radio Ionico será igual al Radio Atómico Calculado, esto es, de 1.56 Angstroms.

El Fe presenta cinco (5) Estados de Oxidación: Fe(2+), Fe(3+), Fe(4+), Fe(5+) y Fe(6+), siendo los más comunes los dos primeros: +2 y +3.

a).- El Fe(2+) o Fe(II) posee un Radio Ionico de 0.76 (Angstrom), en lugar de los 1.56 (A) del Fe(0+), y se encuentra en el compuesto FeO ó Wustita, que al igual que los otros minerales ya antes descritos, encontrados en Sideritos, tiene una estructura cristalina Hexoctaédrico, del Grupo Espacial F m3m.

b).- El Fe(3+) ó Fe(III) posee un Radio Ionico de 0.64 (A), y se encuentra en compuestos como la Maghemita (gamma-Fe2O3), con estructura Isometric-Tetartoidal, del Grupo Espacial P 2(1) 3.

Este estado oxidado para el hierro también lo podemos encontrar el la Magnetita o Fe3O4, cuya fórmula empírica es Fe(3+)2 Fe(2+) O4. De modo similar a las fases minerales halladas en meteoritos, la Magnetita posee estructura cristalina tipo Hexoctaédrica.

c).- El Fe(4+) ó Fe(IV), de Radio Iónico igual a 0.585 (A), es un estado de oxidación del Fe que puede encontrarse en algunos procesos enzimáticos como es el caso de la Enzima Peroxidasa.

d).- El Fe(5+) no está muy bien caracterizado.

e).- El Fe(6+) ó Fe(VI) puede ser hallado en compuestos como el Ferrato de Potasio, K2FeO4, el cual es utilizado como oxidante. Se dice que el Fe(6+) es anfótero, es decir, que como molécula contiene un radical base y otro ácido, pudiendo actuar así como ácido, o como base, según el medio en que se encuentre, tal como sucede con los aminoácidos.

Las sustancias clasificadas como anfóteras tienen la particularidad de que la carga eléctrica de la parte hidrofílica cambia en función del PH del medio. Actúan como bases en medios ácidos y como ácidos en medios básicos, para contrarrestar el PH del medio.